O que são?
Um sistema binário eclipsante é um sistema no qual ambas as estrelas eclipsam uma à outra periodicamente pelo fato do plano orbital delas se encontrar próximo ou na mesma linha de visão do observador. A análise destes sistemas não pode ser realizada diretamente com um telescópio porque a separação entre as estrelas é muito pequena ou eles se encontram muito distantes. Por isso, o sistema só pode ser estudado por meio de espectroscopia e fotometria.
As binárias eclipsantes são estrelas variáveis, não porque a luz individual das estrelas varie, mas devido aos eclipses que estas sofrem.
Por causa da pouca separação entre as estrelas destes sistemas, elas ultrapassam o lóbulo de Roche e realizam transferência de massa, sofrendo também redução em seus períodos orbitais.
Como estudá-las melhor?
Primeiramente, deve-se avaliar a curva de luz do sistema, ou seja, um gráfico que indica a variação do fluxo de luz que o sistema emite para a Terra. Se a curva apresentar um formato senoidal, a órbita do sistema será circular. Se este gráfico apresentar uma forma não senoidal a órbita apresentará uma certa excentricidade. A curva de luz também pode indicar a inclinação do sistema em relação ao plano do céu.
O movimento orbital do sistema gera deslocamento nas linhas espectrais de absorção do sistema do azul e para o vermelho, fazendo o comprimento de onda destas linhas variar, o que nos permite calcular a velocidade radial das duas estrelas.
Quando se pode observar as linhas espectrais das duas estrelas e os seus deslocamentos, isso nos permite obter a velocidade radial de cada uma, analisar com precisão os parâmetros orbitais destas e ainda avaliar a composição química delas.
Estes sistemas podem ser classificados de acordo com a separação entre seus componentes, o raio das estrelas e o seu grau de evolução.
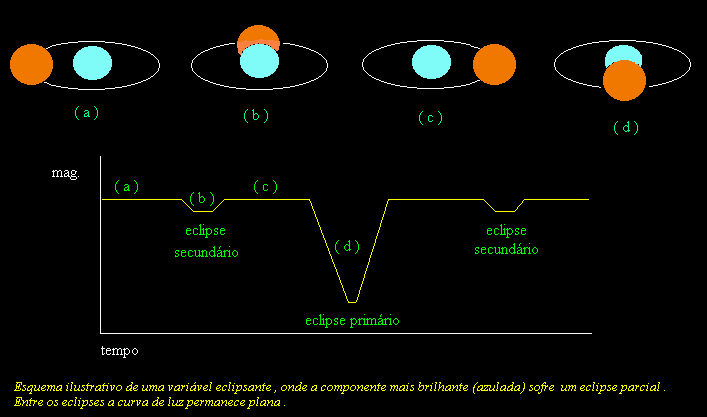
fonte:
http://rea-brasil.org/variaveis/pmf1.htm
Tipos de binárias eclipsantes:
Variáveis Algol
Estes são sistemas que se relacionam com o protótipo desta classe, a estrela Beta Persei ou Algol, em relação do ponto de vista evolucionário. Um binário deste tipo apresenta uma estrela de sequência principal que não preenche o lóbulo de Roche e uma estrela secundária que é maior que a primária, mais fria, menos massiva e que preenche o lóbulo de Roche. O período orbital destas estrelas geralmente é curto porque elas se encontram separadas por uma distância muito pequena.
O período orbital pode variar devido a frenagem magnética, o mecanismo Applegate ou a presença de uma terceira estrela realizando uma órbita excêntrica no sistema. Esta última situação pode provocar enormes variações no período orbital do sistema. Esta variação pode ocorrer em uma questão de décadas ou séculos.
W Ursae Majoris:
As variáveis W Ursae Majoris, também conhecidas como binárias de contato de baixa massa, é um tipo de binária eclipsante com estrelas que pertencem as classes espectrais F, G ou K que compartilham um envelope comum de matéria e, portanto, elas realizam transferência de massa. Elas são chamadas de binárias de contato pelo fato desta transferência ocorrer pelo através do pescoço de conexão entre elas. Por causa da pouca separação entre as estrelas destes sistemas, elas ultrapassam o lóbulo de Roche e realizam transferência de massa, sofrendo também redução em seus períodos orbitais e separação.
Estas variáveis podem ainda ser divididas em subclasses que são: Tipo A, tipo W, tipo B e tipo H.
Primeiramente, as binárias tipo A são compostas de estrelas mais quentes que o Sol, com classes espectrais A e F e períodos orbitais que variam entre 0,4 e 0,8 dias. Os tipo W apresentam estrelas que têm tipos espectrais G e K, o que faz com que elas tenham temperaturas próximas as do Sol e períodos. Os tipos B, introduzidos em 1978, são estrelas que possuem maior diferença de temperatura em suas superfícies. Por fim, o tipo H apresenta estrelas com uma grande diferença de massa e uma razão de massa maior que 0,72.
Fonte:
https://en.wikipedia.org/wiki/Binary_star
Beta Lyrae:
Neste tipo de sistema, ambas as estrelas são muito massivas e grandes. Estas são totalmente distorcidas porque elas se encontram tão próximas que a força mútua de gravitação distorce-as. As estrelas apresentam um formato elipsoidal e há um intenso fluxo de transferência de massa entre elas.
Este último fenômeno ocorre porque uma das estrelas evoluiu e se tornou uma gigante ou super gigante. Tais estrelas perdem massa facilmente porque são muito grandes e, por conta disso, a gravidade em suas superfícies é muito pequena, então rapidamente o gás nelas escapa e é transferida para a estrela menor. Existe um fator que acelera a transferência de massa, a estrela maior pode inchar até preencher o limite de Roche, uma superfície matemática na qual a matéria envolvendo um sistema binário pode fluir livremente de uma estrela para a outra.
Determinação de velocidade radial (efeito Doppler):
Como já dito, o movimento orbital das duas estrelas gera deslocamento nas linhas espectrais de absorção do sistema do vermelho e para o azul. Este deslocamento provoca também um deslocamento do comprimento de onda destas linhas, o que nos permite estudar melhor os sistemas binários espectroscópicos e eclipsantes. Primeiramente deve se calcular a velocidade radial das estrelas por meio da fórmula do efeito Doppler abaixo:
Vr =
Δλ
c λ
Vr= velocidade da onda em (em km/s)
c= velocidade da luz em unidades naturais, logo c=300 000 km/s
λ= comprimento de onda sem deslocamento
Δλ=comprimento de onda observado
Após analisar o gráfico de velocidade do sistema, pode-se obter a semi-amplitude do sistema, ou seja, a velocidade orbital máxima das duas estrelas.
A inclinação afeta a velocidade radial que observamos de modo que:
K= V sen i
K= velocidade máxima da estrela observada
V=velocidade real da estrela
i= inclinação da órbita
Existe um método para determinar K. Ele é dado por:
K=
2π • (a• sen i)
P
Onde:
i= inclinação(em graus)
P=período orbital
a=semieixo maior
K= velocidade máxima observada da estrela (ou semi amplitude)
Esta relação é válida para órbitas circulares, mas para órbitas excêntricas ela é dada por:
K=
2π • (a• sen i)
P
√(1-e^2)
K= velocidade máxima da estrela observada (ou semi amplitude)
e= excentricidade
i= inclinação(em graus)
P=período orbital
a=semieixo maior
Como esta fórmula é mais complexa, é mais fácil obter a velocidade da estrela por meio de observação do próprio sistema.
Outros parâmetros orbitais:
Como já mencionado, a excentricidade e a inclinação a órbita podem ser obtidas por meio do estudo da curva de luz, o período orbital pode ser obtido por meio da observação dos eclipses e a velocidade das duas estrelas é obtida por meio de espectroscopia. Para uma órbita circular com inclinação de 90 graus, o semi eixo maior é dado por:
a= P • (K1+K2)
2π
Onde
P= período orbital do sistema (em segundos)
K1= semi amplitude da estrela primária (em km/s)
K2= semi amplitude da estrela primária (em km/s)
a= semi eixo maior (em km)
Como não existem somente órbitas circulares, é necessária alguma forma de obter as semi amplitudes de órbitas não circulares. Por isso, para uma órbita excêntrica e inclinada, o semi eixo maior é dado por:
a= P • (K1+K2) •√(1-e^2)
2π • sen i
Onde
P= período orbital do sistema (em segundos)
K1= semi amplitude da estrela primária (em km/s)
K2= semi amplitude da estrela primária (em km/s)
a= semi eixo maior (em km)
i= inclinação(em graus)
e= excentricidade
Massa do sistema:
A massa do sistema é dado pela terceira lei de Kepler:
M
1+M
2=
a^3
P^2
a= semi eixo maior (em UA)
P= período orbital do sistema.
M1= massa da estrela primária
M2=massa da estrela secundária
Determinação do raio das estrelas por meio de eclipses:
Sabendo-se a duração dos eclipses, a semi amplitude das estrelas e a forma da curva de luz pode-se determinar o raio das estrelas pelas fórmulas que se encontram na imagem abaixo.
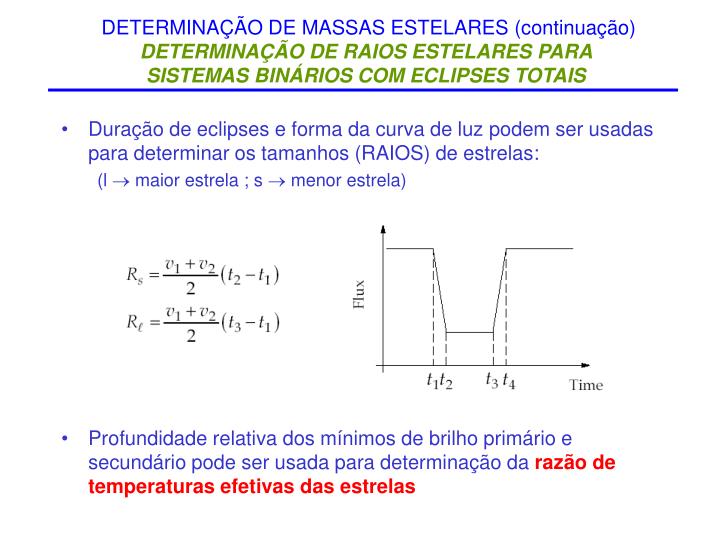
fonte:
https://www.slideserve.com/emmet/teorema-russell-vogt
Onde:
V
1= semi amplitude da estrela primária
V
2= semi amplitude da estrela secundária
t2-
t1= intervalo entre o primeiro e o secundo contato entre as estrelas
t3-t1= intervalo entre o primeiro e o terceiro contato entre as estrelas
Existe outra equação para calcular o raio da estrela maior dada por:
Rg= Rp+(V1+V2) •(
t3-t2)
2
Onde:
Rg=raio da estrela maior
Rp=Raio da estrela menor
V1= semi amplitude da estrela primária
V
2= semi amplitude da estrela secundária
t3-t2=intervalo entre o terceiro e o segundo contato
Nota: V
1=K
1 e V
2=K
2
Exemplo 1:
A análise do espectro de uma binária eclipsante com linhas duplas resulta em um período orbital de 8,6 anos. O máximo deslocamento Doppler da linha de Balmer (igual a 656,281 nm) é
Δλs= 0,072 nm para a estrela menor e de 0,0068 nm para a estrela maior, pela forma senoidal da curva de velocidade, pode-se dizer que a órbita é circular.
dados
Δλs= 0,072 nm
Δλl= 0,0068 nm
P=8,6 anos= 2,712096 • 10^8 s
e=0
c=300 000 km/s
Primeiramente, deve-se calcular a velocidade radial das estrelas do sistema.
Para a estrela menor:
V1=c •
Δλs=300 000 km/s • (0,072 nm/656,281 nm)= 300 000 km/s
• (1,1•10^-4)=33 km/s
λs
Para a estrela maior
V
2=c •
Δλl=300 000 km/s • (0,0068 nm/656,281 nm)= 300 000 km/s • (1,04 • 10^-5)=3,12 km/s
λl
Em relação à órbita
Vt=V
1 + V
2=33+ 3,12=36,12 km/s
a= P • (V1+V2)= (2,712096 • 10^8 s) •36,12 km/s=1 559 096 266 km= 10,4 UA
2π
2π
Usando a terceira de Kepler, podemos determinar a massa total do sistema, pois sabemos o período orbital do sistema e o semieixo maior desta órbita.
M
1 + M
2= a^3/P^2= 10,4^3/8,6^2= 15,2 massas solares
Utilizando-se da razão entre as semi amplitude das duas estrelas, obtemos uma proporção entre a massa individual das duas estrelas.
V
2=
M1=
3,12=0,0945
V
1 M
2 33
Usando esta proporção concluímos que:
M
1/M
2=0,0945
M
1=M
2 • 0,0945= 0,0945 M2
Sabendo a relação entre a massa das duas estrelas, podemos determinar a massa das duas estrelas
M
1+M2=0,0945M2+M2=1,0945 M2=15,2
M
2=
15,2 =13,9 massas solares
1,0945
Por fim, pode-se obter a massa da outra estrela por meio da razão de massa estabelecida entre elas.
M
1=0,0945 M
2= 0,0945 • 13,9= 1,3 massas solares
O estudo da curva de luz deste sistema mostrou que o intervalo entre o primeiro e o segundo contato e entre o primeiro e o terceiro.
Dados
t3-t1=164 horas=14 169 600 s
t2-t1=11,7 horas=42 120 s
Usando a equação do raio da estrela menor temos:
Rp=Vt •
t2-
t1= 18,06 km/s • 42 120 s=760 687,2 km=1,1 Raio solar
2
Usando uma outra fórmula conseguiremos o raio da estrela menor
Rg=Rp+(V1+V2) •(
t3-t2)=760 687,2 km +(18,06 km/s •
14 169 600 s) =369 raios solares
2
Função de massa:
Existem sistemas binários nos quais só podemos observar informações sobre a órbita de apenas um membro deste. Isso pode ocorrer porque pode haver diferenças enormes de luminosidade entre as duas estrelas que podem ser provocadas por razões extremas de massa ou porque um dos componentes é uma anã branca, estrela de nêutrons ou buraco negro. Às vezes, a posição de um dos constituintes do sistema tem a sua posição desconhecida. No caso destes sistemas binários espectroscópicos de linha única, só podemos medir o período orbital do sistema e a semi amplitude da estrela visível. Com estes dados, podemos estimar a massa mínima da estrela não observável do sistema por meio de uma função conhecida como função de massa. Para órbitas circulares, ela é dada por:
f(M2)= (M2)^3 • sen^3 i= P • K1^3
Mt^2 2πG
Onde
f(M2)= função de massa (em unidades de massa)
Mt= massa das duas estrelas
M2= massa da estrela secundária
G= constante gravitacional= 6,674 • 10^-11 m^3 kg^-1 s^-2
P= período orbital ( em segundos)
K1= semi amplitude da estrela primária
Para órbitas excêntricas a função de massa é dada por:
f(M2)= (M2)^3 • sen^3 i= P • K1^3 • √(1-e^2)^ 3/2
Mt^2 2πG
A única diferença entre a primeira fórmula e esta é somente a presença do termo √ (1-e^2)^3/2 na segunda.
Por fim, podemos estimar a função de massa total do sistema a partir das semi amplitudes e seu período orbital. Isso pode ser feito quando não se conhece a inclinação do sistema, pois é apenas uma aproximação do valor real.
Mt • sen^3 i=P • (K1+K2)^3
2πG
Onde
Mt= massa total do sistema.
M2= massa da estrela secundária.
G=constante gravitacional= 6,674 • 10^-11 m^3 kg^-1 s^-2
P= período orbital ( em segundos)
K1= Semi amplitude da estrela primária
K2= Semi amplitude da estrela secundária
Relação massa-luminosidade
Quando colocamos o valor da massa de uma estrela e a sua luminosidade em um gráfico, descobrimos que elas apresentam uma relação empírica conhecida como relação massa-luminosidade.
Esta relação foi descoberta pelo astrônomo inglês Sir Arthur Eddigton. Ela definida por:
L = (M ) ^a
Lsol (Msol)
L=luminosidade da estrela
Lsol=Luminosidade do Sol
M=Massa da estrela
Msol= Massa do sol
a= índice que depende da estrutura da estrela, opacidade das atmosferas e temperaturas.
O valor de a varia conforme o tipo de estrela que é estudada.
a~4 para estrelas com altas massas e luminosidades
a~3,5 para estrelas com massa e luminosidade próximas as do Sol
a~2,3 para estrelas com massa e luminosidade menores que as do Sol
Temperatura efetiva:
Por fim, existe uma maneira de obtermos a temperatura destas estrelas a partir de seus raios e temperaturas a partir da derivação da seguinte fórmula.
L = R/Rsol^2 x T/Tsol^4
Lsol
( T ) ^4=(L/Lsol)/(R/Rsol^2)
(Tsol)
T =
4√(L/Lsol)/(R/Rsol^2)
Tsol
Onde:
T= temperatura na superfície da estrela
Tsol=Temperatura na superfície do sol
L=luminosidade da estrela
Lsol=luminosidade do sol
R=raio da estrela
Rsol=raio solar
Existem outros meios de obter a temperatura na superfície da estrela, mas só vim mostrar este por acreditar que este é mais prático e muitos casos.
Conclusão:
Existem poucas binárias eclipsantes na Via Láctea, pois são raros os sistemas nos quais o seu movimento orbital é realizado na mesma linha de visão da Terra, mas isso não tira o fato de estudos sobre ela serem muito importantes na compreensão do universo.
Agradecimentos:
Agradeço a todos que prestigiarem meu blog e espero que gostem das atuais e futuras postagens. Espero que realmente gostem das futuras postagens e caso alguém tenha alguma dúvida, não tenham medo de comentar. Nestes próximos meses, irei postar algumas postagens sobre alguns sistemas binários eclipsantes, mas também continuarei postando sobre outros assuntos. Por favor, comentem também outros assuntos que vocês gostariam que eu abordasse.
Novamente, agradeço por prestigiarem o blog.
Postarei no blog a cada 15 dias.
Colaboradores:
Pedro Henrique Cintra, Pedro André Menezes de Moraes Amora, Gabriel Galheigo Rabello Sommer.
Autor do artigo:
Gustavo Sobreira Barroso.
Referências:





